Rhyd Lewis

Cardiff School of Mathematics,
Cardiff University, Cardiff, CF24 4AY, WALES.
Tel: +44 2920 874856
Email: LewisR9@cardiff.ac.uk
School webpage | Linkedin | Google scholar | Orcid

Rhyd Lewis

Welcome to my personal webpage. Here, you'll find information on my research, publications, and teaching.

If you would like to contact me, arrange a visit, or are interested in pursuing a PhD, please contact me using the email address above.

Research and Teaching.

Overview

I am a professor at the School of Mathematics in Cardiff University. I am an associate editor for the International Journal of Metaheuristics and a programme committee member for:

• Evolutionary Computation in Combinatorial Optimisation (EVOCOP)
• The Practice and Theory of Automated Timetabling (PATAT)
• The Genetic and Evolutionary Computation Conference (GECCO)

Research Interests

• Algorithmic graph theory and combinatorial optimisation
• Graph colouring
• Heuristics and integer programming
• Vehicle routing and arc routing
• Shortest path algorithms
• School bus routing
• Applications of operational research in agriculture
• Automated timetabling and related problems
• Grouping and partitioning problems
• Operating theatre scheduling
• Sports scheduling
• Solving Latin square and Sudoku problems
• Bin packing, trapezoid (trapezium) packing, and the equal-piles problem.

Teaching

I am a fellow of the Higher Education Academy. Currently, I am teaching the following modules at Cardiff University: MA3602 Algorithms and Heuristics, and MA2760 Mathematical Investigations in Python. Previous modules include: MAT002 Statistical Methods; MA0276 Visual Basic for Operational Research; MAT004 Computational Methods; MA0105 Foundations of Probability; BSP658 Business Statistics; BS0511 Quantitative Methods for Business; and BS1501 Applied Statistics and Mathematics for Economics and Business.

Publications.

Books, Journal Articles and Chapters

2024

• Corcoran, P. and R. Lewis (2024) 'Optimisation of Livestock Routing on Farms'. Computers & Industrial Engineering, vol. 188, 109882.

2023

• Lewis, R., P. Corcoran, and A. Gagarin (2023) 'Methods for Determining Cycles of a Specific Length in Undirected Graphs with Edge Weights'. Journal of Combinatorial Optimization, vol. 46, 29.
• Corcoran, P. and R. Lewis (2023) 'A Navigability Entropy Model for Street Networks'. Environment and Planning B: Urban Analytics and City Science, vol. 50(8), pp. 2171-2186.
• Sciortino, M., R. Lewis, and J. Thompson (2023) 'A School Bus Routing Heuristic Algorithm Allowing Heterogeneous Fleets and Bus Stop Selection'. Springer Nature Computer Science, vol. 4, 74.

2022

• Thiruvady, D. and R. Lewis (2022) 'Recombinative Approaches for the Maximum Happy Vertices Problem'. Swarm and Evolutionary Computation, vol. 75, 101188.
• Lewis, R. and P. Corcoran (2022) 'Finding Fixed-Length Circuits and Cycles in Undirected Edge-Weighted Graphs: An Application with Street Networks'. Journal of Heuristics, vol. 28, pp. 259-285.
• Hawa, A., R. Lewis and J. Thompson (2022) 'Exact and Approximate Methods for the Score-Constrained Packing Problem'. European Journal of Operational Research, vol. 302(3), pp. 847-859.

2021

• Lewis, R. (2021) A Guide to Graph Colouring: Algorithms and Applications (second ed.). Springer. ISBN: 978-3-030-81053-5.
• Lewis, R., D. Thiruvady and K. Morgan (2021) 'The Maximum Happy Induced Subgraph Problem: Bounds and Algorithms'. Computers and Operations Research, vol. 126, 105114.
• Sciortino, M., R. Lewis, and J. Thompson (2021) 'A Heuristic Algorithm for School Bus Routing with Bus Stop Selection'. In Evolutionary Computation in Combinatorial Optimization (Lecture Notes in Computer Science vol. 12692), Springer, pp. 202-218.
• Kheiri, A., R. Lewis, J. Thompson, and P. Harper (2021) 'Constructing Operating Theatre Schedules using Partitioned Graph Colouring Techniques'. Health Systems, vol. 10(4), pp. 286-297.

2020

• Lewis, R. (2020) 'Algorithms for Finding Shortest Paths in Networks with Vertex Transfer Penalties'. Algorithms, vol. 13(11), 269.
• Lewis, R. (2020) 'A Heuristic Algorithm for Finding Attractive Fixed-Length Circuits in Street Maps'. In Computational Logistics (Lecture Notes in Computer Science vol. 12433), Springer, pp. 384-395.
• Lewis, R. (2020) 'A Shortest Path Algorithm for Graphs Featuring Transfer Costs at Their Vertices'. In Computational Logistics (Lecture Notes in Computer Science vol. 12433), Springer, pp. 539–552.
• Padungwech, W., J. Thompson and R. Lewis (2020) 'Effects of Update Frequencies in a Dynamic Capacitated Arc Routing Problem'. Networks, vol. 76(4), pp. 522-538.
• Neis, P. and R. Lewis (2020) 'Evaluating the Influence of Parameter Setup on the Performance of Heuristics for the Graph Colouring Problem'. International Journal of Metaheuristics, vol. 7(4), pp. 352-378.
• Lewis, R., T. Anderson and F. Carroll (2020) 'Can School Enrolment and Performance be Improved by Maximizing Students’ Sense of Choice in Elective Subjects?'. Journal of Learning Analytics, vol. 7(1), pp. 75-87.
• Thiruvady, D., R. Lewis and K. Morgan (2020) 'Tackling the Maximum Happy Vertices Problem in Large Networks'. 4OR, vol. 18, pp. 507-527.

2019

• Lewis, R., D. Thiruvady and K. Morgan (2019) 'Finding Happiness: An Analysis of the Maximum Happy Vertices Problem'. Computers and Operations Research, vol. 103, pp. 265-276.

2018

• Lewis, R. and K. Smith-Miles (2018) 'A Heuristic Algorithm for Finding Cost-Effective Solutions to Real-World School Bus Routing Problems'. Journal of Discrete Algorithms, vol. 52-53, pp. 2-17.
• Hardy, B., R. Lewis, and J. Thompson (2018) 'Tackling the Edge Dynamic Graph Colouring Problem with and without Future Adjacency Information'. Journal of Heuristics, vol. 24(3), pp. 321-343.
• Lewis, R., K. Smith-Miles, and K. Phillips (2018) 'The School Bus Routing Problem: An Analysis and Algorithm'. In Combinatorial Algorithms (Lecture Notes in Computer Science vol. 10765), Springer, pp. 287-298.
• Hawa, A., R. Lewis and J. Thompson (2018) 'Heuristics for the Score-Constrained Strip-Packing Problem'. In Combinatorial Optimization and Applications (Lecture Notes in Computer Science vol. 11346), Springer, pp. 449-462.

2017

• Lewis, R. and P. Holborn (2017) 'How to Pack Trapezoids: Exact and Evolutionary Algorithms'. IEEE Transactions on Evolutionary Computation, vol. 21(3), pp. 463-476.

2016

• Lewis, R. (2016) 'Graph Colouring: An Ancient Problem with Modern Applications'. Impact Magazine from The Operational Research Society, Palgrave Macmillan, Spring, pp. 47-50.
• Lewis, R. and F. Carroll (2016) 'Creating Seating Plans: A Practical Application'. Journal of the Operational Research Society, vol. 67(11), pp. 1353-1362.
• Padungwech, W., J. Thompson, and R. Lewis (2016) 'Investigating Edge-Reordering Procedures in a Tabu Search Algorithm for the Capacitated Arc Routing Problem'. In Hybrid Metaheuristics (Lecture Notes in Computer Science vol. 9668), Springer-Verlag, pp. 62-74.
• Hardy, B., R. Lewis, and J. Thompson (2016) 'Modifying Colourings Between Time-steps to Tackle Changes in Dynamic Random Graphs'. In Evolutionary Computation in Combinatorial Optimization (Lecture Notes in Computer Science vol. 9595), Springer-Verlag, pp. 186-201.

2015

• Lewis, R. (2015) A Guide to Graph Colouring: Algorithms and Applications (first ed.). Springer. ISBN: 978-3-319-25728-0.
• Lewis, R. and J. Thompson (2015) 'Analysing the Effects of Solution Space Connectivity with an Effective Metaheuristic for the Course Timetabling Problem'. European Journal of Operational Research, vol. 240, pp. 637-648.
• Lewis, R. (2015) 'Graph Coloring and Recombination'. Springer Handbook of Computational Intelligence, J. Kacprzyk and W. Pedrycz (Eds.), pp. 1239-1254, ISBN: 978-3-662-43504-5.

2014

• Smith-Miles, K., D. Baatar, B. Wreford, and R. Lewis (2014) 'Towards Objective Measures of Algorithm Performance Across Instance Space'. Computers and Operations Research, vol. 45, pp. 12-24.
• John, M., C. Mumford, and R. Lewis (2014) 'An Improved Multi-objective Algorithm for the Urban Transit Routing Problem'. In Evolutionary Computation in Combinatorial Optimization (Lecture Notes in Computer Science vol. 8600), Springer-Verlag, pp. 49-60.

2013

• Carroll, F. and R. Lewis (2013) 'The "Engaged" Interaction: Important Considerations for the HCI Design and Development of a Web Application for Solving a Complex Combinatorial Optimization Problem'. World Journal of Computer Application and Technology, vol. 1(3), pp. 75-82.

2012

• Holborn, P. L., J. M. Thompson, and R. Lewis (2012) 'Combining Heuristic and Exact Methods to Solve the Vehicle Routing Problem with Pickups, Deliveries and Time Windows'. In Evolutionary Computation in Combinatorial Optimization (Lecture Notes in Computer Science vol. 7245), Springer-Verlag, pp. 63-74.
• Lewis, R., J. Thompson, C. Mumford, and J. Gillard (2012) 'A Wide-Ranging Computational Comparison of High-Performance Graph Colouring Algorithms'. Computers and Operations Research, vol. 39(9), pp. 1933-1950.
• Song, X., R. Lewis, J. Thompson, and Y. Wu (2012) 'An Incomplete m-Exchange Algorithm for Solving the Large-scale Multi-Scenario Knapsack Problem'. Computers and Operations Research, vol. 39(9), pp. 1988-2000.
• Lewis, R. (2012) 'A Time-Dependent Metaheuristic Algorithm for Post Enrolment-based Course Timetabling'. Annals of Operations Research, vol. 194(1), pp. 273-289.

2011

• Lewis, R., X. Song, K. Dowsland, and J. Thompson (2011) 'An Investigation into two Bin Packing Problems with Ordering and Orientation Implications'. European Journal of Operational Research, vol. 213, pp. 52-65.
• Lewis, R. and E. Pullin (2011) 'Revisiting the Restricted Growth Function Genetic Algorithm for Grouping Problems'. Evolutionary Computation, vol. 19(4), pp. 693-704.
• Lewis, R. and J. Thompson (2011) 'On the Application of Graph Colouring Techniques in Round-Robin Sports Scheduling'. Computers and Operations Research, vol. 38(1), pp. 190-204.

2010

• McCollum, B., A. Schaerf, B. Paechter, P. McMullan, R. Lewis, A. Parkes, L. Di Gaspero, R. Qu, and E. Burke (2010) 'Setting The Research Agenda in Automated Timetabling: The Second International Timetabling Competition'. INFORMS Journal on Computing, vol. 22(1), pp. 120-130.
• Song, X., C. Chu, R. Lewis, Y. Nie, and J. Thompson (2010) 'A Worst Case Analysis of a Dynamic Programming-based Heuristic Algorithm for 2D Unconstrained Guillotine Cutting'. European Journal of Operational Research, vol. 202(2), pp. 368-378.

2009

• Lewis, R. (2009) 'A General-Purpose Hill-Climbing Method for Order Independent Minimum Grouping Problems: A Case Study in Graph Colouring and Bin Packing'. Computers and Operations Research, vol. 36(7), pp. 2295-2310.

2008

• Lewis, R. (2008) 'A Survey of Metaheuristic-based Techniques for University Timetabling Problems'. OR Spectrum, vol. 30(1), pp. 167-190.

2007

• Lewis, R. (2007) 'Metaheuristics can Solve Sudoku Puzzles'. Journal of Heuristics, vol. 13 (4), pp. 387-401.
• Lewis, R., and B. Paechter. (2007) 'Finding Feasible Timetables Using Group-Based Operators'. IEEE Transactions on Evolutionary Computation, vol. 11(3), pp. 397-413.
• Lewis, R., B. Paechter, and O. Rossi-Doria (2007) 'Metaheuristics for University Course Timetabling'. In Evolutionary Scheduling (Studies in Computational Intelligence, vol. 49), K. Dahal, Kay Chen Tan, P. Cowling (Eds.) Berlin: Springer-Verlag, pp. 237-272.
• Lewis, R. (2007) 'On the Combination of Constraint Programming and Stochastic Search: The Sudoku Case'. In Hybrid Metaheuristics (Lecture Notes in Computer Science vol. 4771) T. Bartz-Beielstein, M. Aguilera, C. Blum, B. Naujoks, A. Roli, G. Rudolph, and M. Sampels (Eds.) Berlin: Springer-Verlag, pp. 96-107.

2006

• Lewis, R. (2006) 'Metaheuristics for University Course Timetabling'. Doctoral Thesis, Napier University, Edinburgh, Scotland.

2005

• Lewis, R. and B. Paechter (2005). 'Application of the Grouping Genetic Algorithm to University Course Timetabling'. In Evolutionary Computation in Combinatorial Optimization (Lecture Notes in Computer Science vol. 3448), J. Gottlieb and G. Raidl (Eds.), Berlin: Springer-Verlag, pp. 144-153.

Selected Presentations

• Two Example Optimisation Problems from the World of Education. Keynote talk given at the OR Society Annual Conference (OR60), Lancaster University, Lancaster, September 2018.
• Bin Packing with Trapezia: Methods and Applications. Talk given at the 15th European Special Interest Group on Cutting and Packing (ESICUP) Workshop, Zoetermeer, Netherlands, May 2018.
• Applying Set Partitioning Methods in the Construction of Operating Theatre Schedules. Talk given at the International Conference on Theory and Practice in Modern Computing (TPMC) 2015, Las Palmas de Gran Canaria, July 2015.
• A Survey of Various High-Performance Graph Colouring Algorithms and Related Timetabling Issues. Keynote talk given at the OR Society Annual Conference (OR53), Nottingham University, Nottingham, September 2011.
• An Introduction to Metaheuristic Algorithms and the Problems they (try to) Solve. Keynote talk given at the British Computing Society Lecture, Cardiff Business School, October 2008.

Completed PhD Projects

• Hawa, A. (2020) "Exact and evolutionary algorithms for the score-constrained packing problem".
• Hardy, B. (2018) "Heuristic methods for colouring dynamic random graphs".
• Padungwech, W. (2018) "Heuristic algorithms for dynamic capacitated arc routing".
• John, M. (2016) "Metaheuristics for designing efficient routes and schedules for urban transportation networks".
• Rowse, E. (2015) "Robust optimisation of operating theatre schedules".
• Holborn, P. (2013) "Heuristics for dynamic vehicle routing problems with pickups and deliveries and time windows".
• Taylor, L. (2013) "Local search methods for the post enrolment-based course timetabling problem".

Resources.

The following subsections give "beginner's guides" to some of my research interests. Further information can be found by following the links and consulting the relevant publications above.

Graph Colouring:

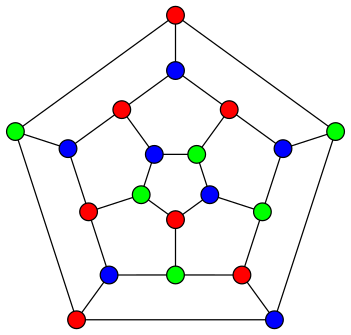Illustration of the Graph Colouring Problem Graph colouring is the task of colouring the vertices of a graph so that (a) all pairs of adjacent vertices are assigned different colours, and (b) the number of different colours used is minimal. For example, the image on the right shows a solution using just three colours, which is the minimum number for this particular graph. The graph colouring problem has applications in many practical areas including university timetabling, sports scheduling, creating seating plans, and solving Sudoku puzzles. It is also related to the four colour theorem which, for over one hundred years, was one of the most famous unsolved problems in all of mathematics.

For further information on graph colouring and its applications, please refer to my book A Guide to Graph Colouring: Algorithms and Applications. The suite of graph colouring algorithms used in this book is available here.

Some short introductory videos on graph colouring can also be found at the following links:

• An Introduction to Graph Colouring;
• Constructive Algorithms for Graph Colouring;
• Practical Applications of Graph Colouring.

School Bus Routing:

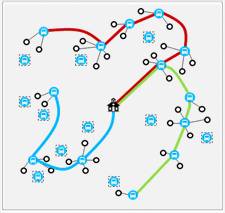Illustration of the school bus routing problem The school bus routing problem involves compiling a list of eligible students, and then efficiently organising their transport to school. This process requires the selection of a suitable set of pick-up points (bus stops), the assignment of students to these pick-up points, and the creation of bus routes that visit these stops while getting students to school on time. In doing this, four factors should be considered: (1) We should try to reduce economic costs by minimising the number of vehicles used; (2) Bus journeys should not be too long for students; (3) Pick-up points should be close to people’s houses; (4) Buses should not be over-filled.

This problem is an interesting mix of vehicle routing, set covering, and bin packing. Some of my publications have looked at producing effective heuristics for this problem. Further details, including visualisations of problems and a suite of benchmark problem instances, can be found on a dedicated webpage here.

Trapezoid Packing:

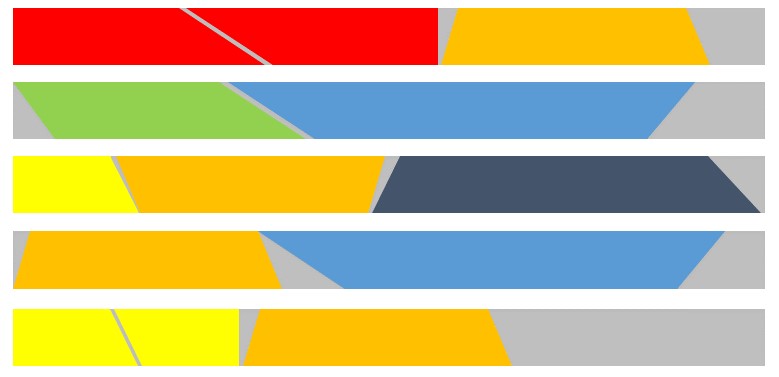Example of a Trapezoid Packing Problem The trapezoid packing problem is closely related to the one-dimensional bin packing problem. Here, items are trapezoidal in shape with a fixed height and variable width. A practical application arises in the roofing industry, where large numbers of roof trusses of different lengths and different "end angles" have to be cut from boards of a given length such that wastage is minimised. Though similar to one-dimensional bin packing, the problem is complicated by the fact that the ends of the trapezoids need to be "nested" so that wastage between consecutive shapes is kept to a minimum.

In my 2016 publication 'How to Pack Trapezoids: Exact and Evolutionary Algorithms' I gave the first polynomial-time exact algorithm for packing items optimally into a single bin. This exact algorithm was then used as part of a wider algorithm for finding high-quality solutions to the multi-bin problem. The source code and a detailed breakdown of the results of this work is available here. Some of these algorithms have since been used in the AutoBarSizer software created by the Fraunhofer Institute for Algorithms and Scientific Computing.

Fixed-length routing

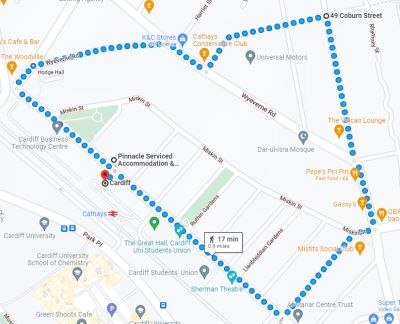Shortest Path Problem with Transfer Penalties In this problem we want to construct fixed-length round trips on street networks. This has several real-world applications such as planning a jogging route, or determining a walk that allows a user to complete their daily steps quota. Although quite simple sounding, this problem can be very difficult to solve, particularly if users want to avoid visiting the same locations repeatedly. If routes cover large geographical areas, the underlying road networks can also be very large, greatly increasing computational requirements. Adjustments also need to be made for different modes of travel modes such as walking, cycling, and driving.

In recent work (currently under review) several effective and fast fast-acting heuristics have been designed for this problem. The table below links to solutions produced by these algorithms for some famous landmarks.

Landmark	5 km	10 km	50 km
Arc de Triomphe, France	Link	Link	Link
Niagara Falls, Canada	Link	Link	Link
Cardiff Castle, Wales	Link	Link	Link
Melbourne Cricket Ground, Australia	Link	Link	Link

Shortest Path Problems

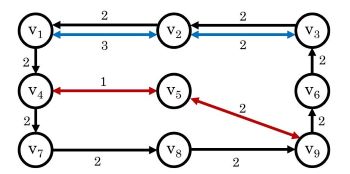Shortest Path Problem with Transfer Penalties The shortest path problem involves finding the most efficient way of travelling between two points in a network. It is most commonly used in online mapping tools and vehicle navigation systems, although applications also exist in social network analysis, currency exchange, and arbitrage.

Several well-known polynomial-time methods are available for the shortest path problem, including the Bellman-Ford algorithm, Dijkstra's algorithm, and the A* algorithm. In many real-world applications, however, complications can arise due to the occurrence of "transfer penalties" at the vertices. Consider the graph on the right, which depicts a small public transport system with edge colours representing transport lines and weights representing travel times. Suppose that we want to find the shortest path from vertex v₁ to v₉ in this graph. By inspection, this is (v₁, v₄, v₅, v₉) with a length of 2 + 1 + 2 = 5. However, this path involves changing lines at v₄ which, might incur some time penalty (e.g., if the commuter needs to change vehicles). If this penalty is more than three units, then the shortest path from v₁ to v₉ now becomes (v₁, v₄, v₇, v₈, v₉) with a length of eight.

In this 2020 paper (pdf), several polynomial-time algorithms are proposed that efficiently solve this extension to the shortest path problem.

Constructing Operating Theatre Schedules:

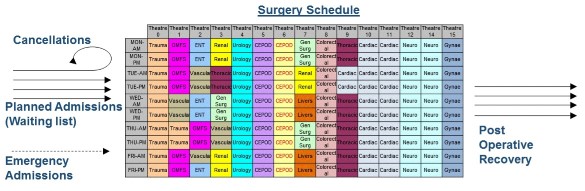Operating Theatre Scheduling When a patient enters a hospital for an elective operation, a bed must be available for them to be put into after surgery. However, sometimes all beds in the ward will be occupied, meaning that the operation will have to be cancelled. Our research has shown that cancellations occur far less frequently if operations are scheduled throughout the week according to a strategically designed master surgery schedule. As part of this, we also must take into account various hospital requirements, the unexpected arrival or emergency patients, and the variability in the time patients take to recover after their operations. Further information can be found in this paper.

Happy Colouring and Graph Homophily:

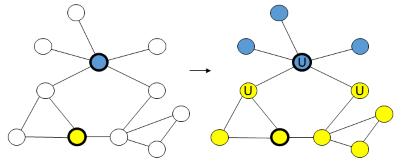Illustration of the Maximum Happy Vertices Problem Another problem that involves colouring vertices in a graph is the maximum happy vertices problem. Here, we are given a graph in which some of the vertices are already coloured (as with the left graph in the figure). Our task is to then colour the remaining vertices so that they are given the same colour as all of their neighbours. In the example solution on the right, we see that most vertices are "happy" because they are the same colour as their neighbours. However, because of the colourings specified in the original graph, it is not possible for all vertices to be happy. (Unhappy vertices are marked with a "U".) This sort of problem is useful in identifying community structures in social networks, amongst other things. See this paper for further details.

Wedding Seat Planning

In the mid-2010's I was involved in the creation of the commercial website www.weddingseatplanner.com. This service provides an interactive online tool for designing optimal seating plans for weddings and other large gatherings. 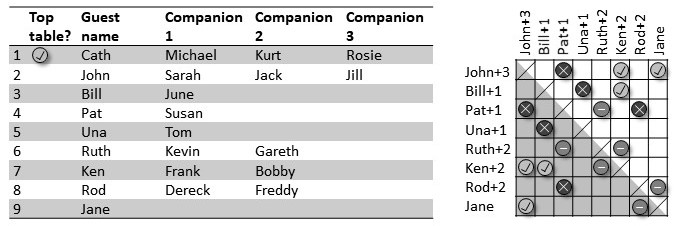Wedding Seat Planner Interface The optimisation algorithms used for this tool were originally programmed in ActionScript and are described in my 2021 book A Guide to Graph Colouring: Algorithms and Applications. They also appear in this 2016 paper.

Since 2020, Adobe has removed all support for Flash Player, meaning that this tool no longer runs on most web browsers. I have therefore made available a C++ version of the same optimisation algorithm, which can be downloaded from here . This implementation allows a repetition of all of the experiments reported in the above publications.

Timetabling

Some of my research has focussed on the production of efficient algorithms for university and school timetabling problems. A large number of timetabling problem instances are available for this problem due to the International Timetabling Competition. Some hard timetabling instances can also be found here. This latter set contains sixty problem instances of varying sizes that are intended to be more difficult than the competition instances with regards to both finding feasibility and satisfying soft constraints. Source code and results for the algorithm presented in Lewis, R. and J. Thompson (2015) 'Analysing the Effects of Solution Space Connectivity with an Effective Metaheuristic for the Course Timetabling Problem'. European Journal of Operational Research, vol. 240, pp. 637-648 can be found here

Sudoku:

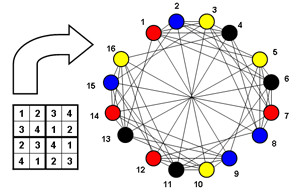Converting Sudoku into Graph Colouring Some of my work has concerned the use of metaheuristics to help solve Sudoku puzzles. The C++ code used for experiments described in "Lewis, R. (2007). 'Metaheuristics can Solve Sudoku Puzzles' Journal of Heuristics, vol. 13 (4), pp. 387-401", can be downloaded here. Code for the random sudoku problem instance generator used in this research can be downloaded here.

Regarding Sudoku, here is a very useful Sudoku to Graph Colouring Converter. This program reads in a single Sudoku problem (from a text file) and converts it into the equivalent graph colouring problem. The output file appears in the DIMACS format which can then be used as the input file for any suitable graph colouring algorithm. If a solution using the correct number of colours is found, this can then be easily converted back into the Sudoku representation, giving a valid solution to the original problem.

Travelling Salesman Problem Demonstration:

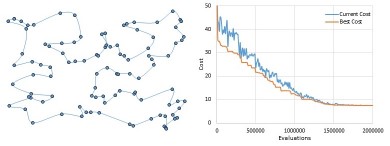Screenshot of Excel TSP Program The travelling salesman problem (TSP) asks the following: "Given a set of cities with distances between each pair, what is the shortest tour that visits each city exactly once?" This is a famous example of an NP-hard problem that is often used in teaching to help motivate the use of heuristics and metaheuristics. To these ends, here is a simple Microsoft Excel program for finding approximate solutions to randomly generated Euclidean TSPs. This program is intended to show students the run-time characteristics of (1) random descent, (2) simulated annealing, (3) steepest descent, (4) tabu search, and (5) evolutionary algorithms. Animated charts are also included in the program to help illustrate algorithm behaviour.

Make a Large Distance Matrix:

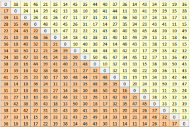Many transportation problems in operational research, such as the travelling salesman problem and vehicle routing problem, make use of a distance matrix. This is a matrix that gives the optimal driving distance (or travel time) between all pairs of locations being considered. A small number of online services exist for producing distance matrices, such as the Google Maps Distance Matrix API, but the sizes of matrices offered are usually very limited. To these ends, here is my own program for producing large distance matrices and travel time matrices. This program is coded in C# and uses Bing Maps to produce matrices of up to 1079x1079 entries in a single sitting. Larger matrices can also be produced, though users should ensure they do not exceed the Bing daily usage limit (see the instructions within the attachment).

Visualising Sociograms:

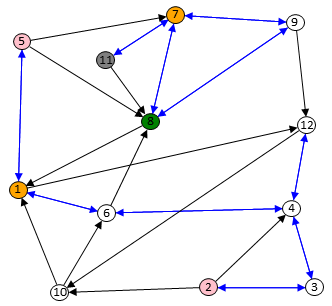An example sociogram A sociogram is a graphical representation of social links between people. The example on the right shows data collected in a small classroom. Each node represents a student and arrows indicate friendships. Black arrows indicate that A likes B, and double-headed blue arrows indicate that both A and B like each other. Colours on the nodes are also used to indicate students that are popular (green), rejected (grey), controversial (orange) and neglected (pink). These classifications are based on the work of Robin Banerjee, found here.

An easy-to-use Excel-based tool for creating sociogram visualisations can be found by following this link. When drawing the network, the program uses a variant of simulated annealing to decide where to place each node on the plane, making the network easier to interpret visually. The cost function of this algorithm seeks to ensure a suitable balance between five criteria: (a) the arrows should not be too long; (b) pairs of arrows should not cross; (c) nodes should be spread out evenly; (d) nodes should not be too close to the border; and (e) arrows should not pass too closely to other nodes. If you want to know more about this optimisation algorithm, please contact me.

Optimising Subject Options Columns:

An example set of options columns 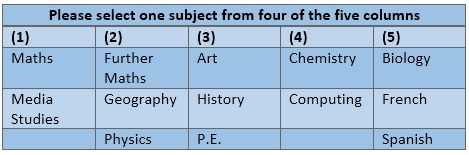In many countries, school students entering their final years of study will be asked to choose a small set of elective subjects. In places such as the United States (APs), Germany (Arbiturs), England and Wales (GCSEs and A-levels), and Australia (HSEs), these choices will be given in a set of "options columns".

The way that subjects are split into options columns is important for schools and students for several reasons.

• Where schools compete for numbers, students are more likely to choose institutions that allow them to study their favoured combination of subjects.
• Allowing students to select their preferred subjects is beneficial for their studies.
• Maximizing the number of students whose choices are satisfied reduces the need for schools to be forced into creating additional classes (and incur the associated financial costs).

In 2020 I published a paper on the topic of optimising subject options columns for schools so that the number of students whose preferences are met is maximised. This research involved creating a free, easy-to-use Excel tool, which can be downloaded here. Further information on this topic can be found on this page.

Photos.

Presenting at the Hay Festival of Literature and the Arts, 2017.

Surfing a secret spot somewhere in south-west Wales

Surfing a beach break near my home

At Surf Snowdonia

Snowboarding (badly) in Austria

Bodyboarding at The Wave, Bristol

Rhyd Lewis

Research and Teaching.

Overview

Research Interests

Teaching

Publications.

Books, Journal Articles and Chapters

2024

2023

2022

2021

2020

2019

2018

2017

2016

2015

2014

2013

2012

2011

2010

2009

2008

2007

2006

2005

Other Selected Articles

Selected Presentations

Completed PhD Projects

Resources.

Graph Colouring:

School Bus Routing:

Trapezoid Packing:

Fixed-length routing

Shortest Path Problems

Constructing Operating Theatre Schedules:

Happy Colouring and Graph Homophily:

Wedding Seat Planning

Timetabling

Sudoku:

Travelling Salesman Problem Demonstration:

Make a Large Distance Matrix:

Visualising Sociograms:

Optimising Subject Options Columns:

Photos.